时间序列预测简介 - 分析过去,预测未来
时间序列预测简介 - 分析过去,预测未来
什么是时间序列分析
时间序列,顾名思义,就是在时间轴上的一系列数据点。所谓时间序列预测,就是利用统计学模型,通过历史数据预报未来数据点的过程。
数据点显然有两个要素,分别是时间要素和数值要素。
若数值累加后仍有意义,则称数据系列是时期序列,否则称时点序列。
时间序列分析在商业,科学等多个领域有重要的实际作用。
时间序列数据的不同组分
时间序列分析在分析有一定规律的数据时才有较好的效果。而现实生活中的很多指标往往都有明确的规律,比如,游乐园的游客人数往往和节假日相关。
传统理论中,时间序列数值变化有以下四个组分
- 长期变动趋势 T
- 季节(月级规模的周期)变动规律,也称季节性调整因子 S(SAF)
- 周期(指更高频)变动规律 C
- 不规则变动(随机扰动项,或残差、误差值)I(ERR)
四种变动与指标数值最终变动的关系可能是叠加关系,也可能是乘积关系。
如果四种变动之间是相互独立,则相加。如果四种变动之间存在相互影响关系,则相乘。
(1)数据具有年内的周期性时才能使用时间序列分解,例如数据是月份数据(周期为12)、季度数据(周期为4) ,如果是年份数据则不行。
(2)在具体的时间序列图上,如果随着时间的推移,序列的季节波动变得越来越大,则反映各种变动之间的关系发生变化,建议使用乘积模型;反之,如果时间序列图的波动保持恒定,则可以直接使用叠加模型;当然,如果不存在季节波动,则两种分解均可以。
时间序列分析的结果常以四种变动因子之间的组合(加或乘)呈现,比如
- 季节性调整后序列(SAS, T+C+I)
- 趋势循环成分(STC,T+C)
详细的理论研究不是我在团队里的职责。下面,我将展示如何用开源软件进行时序预测。
使用 Prophet 进行时序预测
Prophet 时 Facebook 开发的开源时序预测库。下面将以"女装销售数据"(课后作业)为例,进行时间序列预测和简要分析。
首先,打开数据集,用SPSS画出时序图并观察
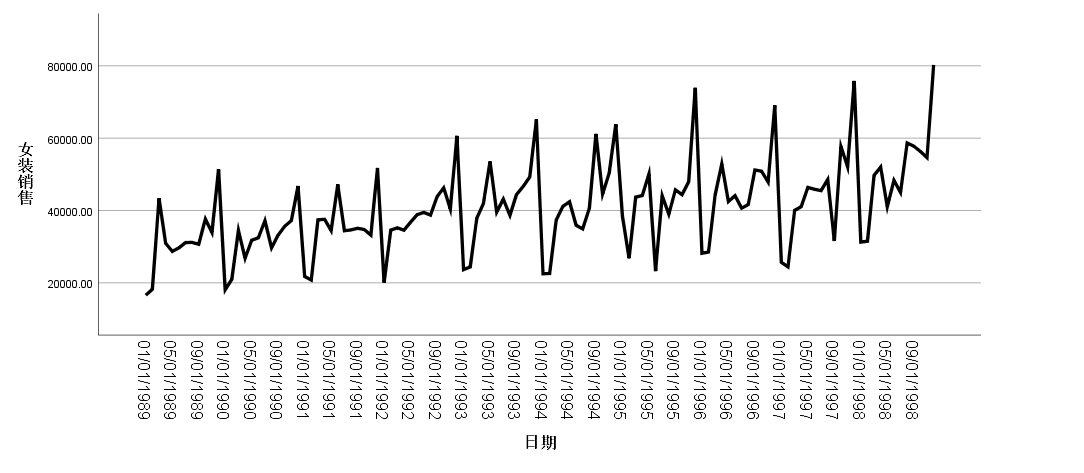
可以看到,女装销售具有总体向上的趋势,且具有一定的季节性规律,符合我们的常识,故可以用现成的模型进行预测。
在SPSS中导出数据,就可以用开源库进行预测了。
首先,引入依赖并导入数据
from prophet import Prophet
import pandas as pd
df = pd.read_csv("Sales_Data.csv")
创建预测器实例
m = Prophet(
mcmc_samples=600,
seasonality_mode="multiplicative",
yearly_seasonality=True,
weekly_seasonality=False,
daily_seasonality=False,
)
m.add_country_holidays(country_name='US')
按月给出的数据属于较低频数据。根据 Prophet 的文档,需要对数据进行重采样后,才能够运行预测。这里,只需要在预测时给出参数即可。显然,对于有趋势的数据,我们的季节性应选择乘法模型模式。
根据上面的观察,每年年末都会出现消费的尖峰,我们猜测是圣诞节,故添加美国的节日列表,让预测器能够处理突发事件。
调整好参数之后,就可以运行自动预测了。
m.fit(df)
拟合完成之后,就可以进行预测。输入预测未来的12个数据点,生成时间戳数据帧,然后运行预测即可。这里,1MS 指定的是我们给出的数据点只在每月初。
future = m.make_future_dataframe(periods=12, freq='1MS')
forecast = m.predict(future)
运行完毕之后,我们可以观察预测的结果和模型拟合的序列分量。
m.plot(forecast)
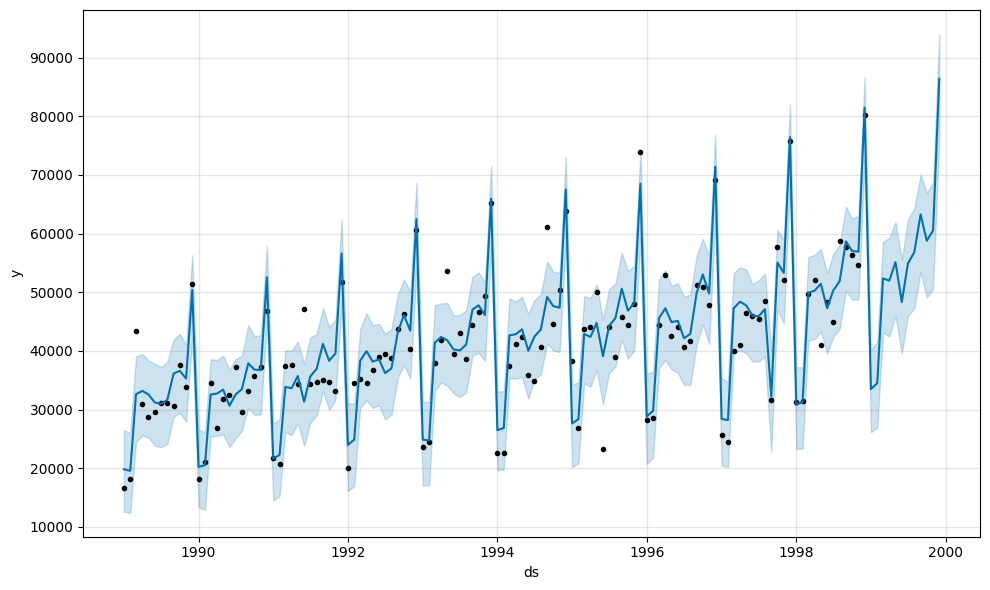
可以看到预测未来一年的曲线形状和以前大致相似,但是存在一定的不确定范围。
然后,我们观察以下程序拟合出的分量
m.plot_components(forecast)
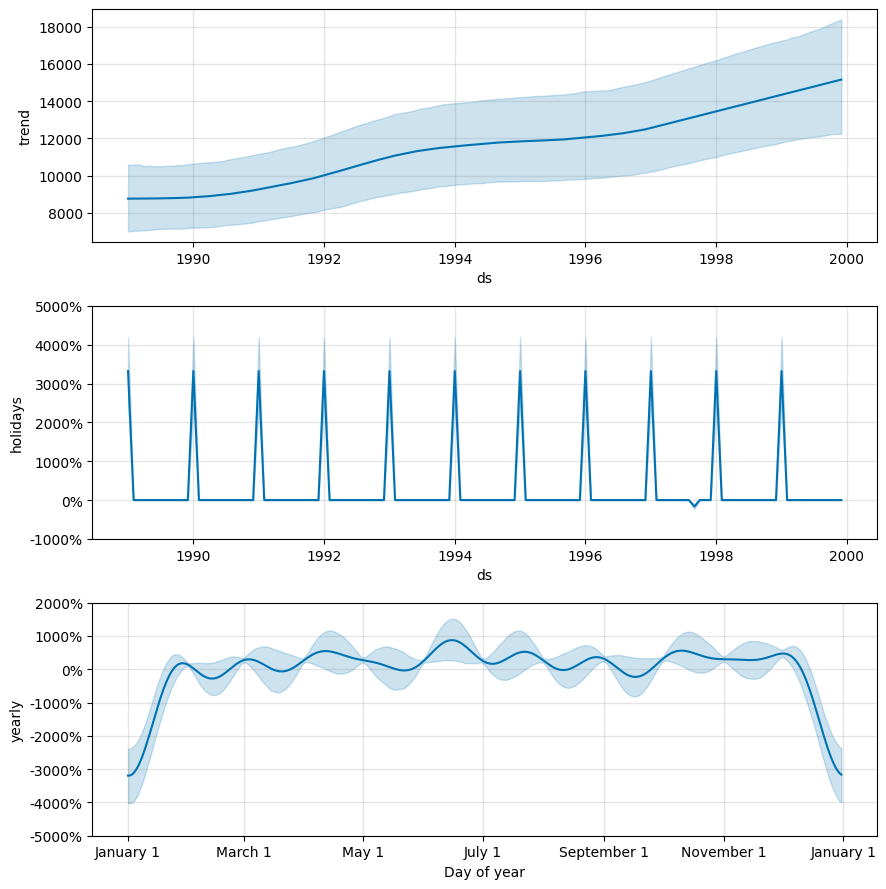
趋势分量逐年上升,符合我们的常识。季节分量也符合我们的常识,每年年末都会有一个尖峰,可以解释成圣诞节的影响。
但是,数据中仍存在噪声,使得结果的不确定度较大。
我们尝试将离群点标记为节日,然后重新运行拟合。
spikes = pd.DataFrame(
{
"holiday": "spikes",
"ds": pd.to_datetime(["3/1/1989", "6/1/1991", "5/1/1993", "9/1/1994"]),
"lower_window": 0,
"upper_window": 20,
}
)
重新运行的结果如下
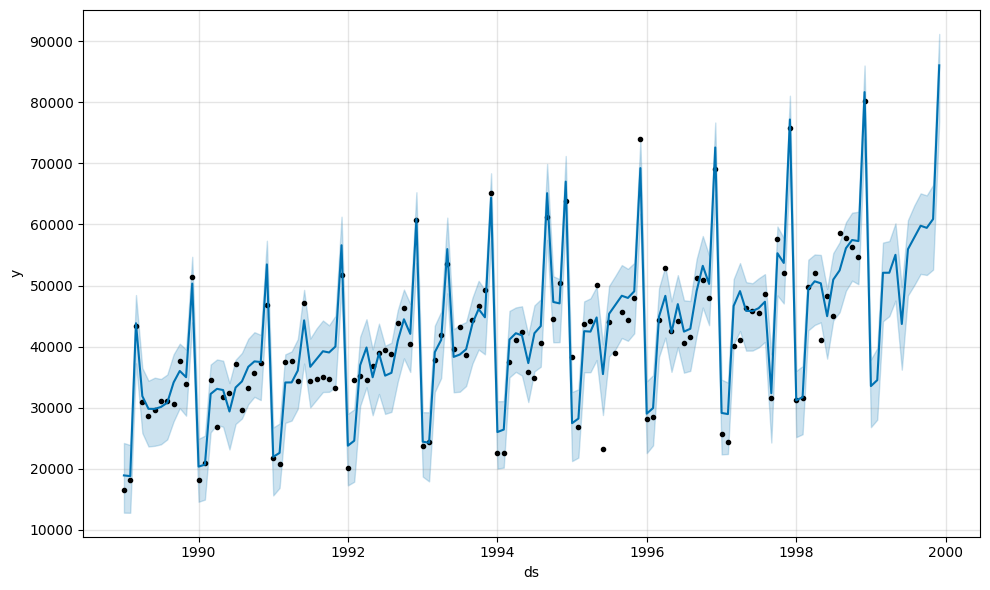
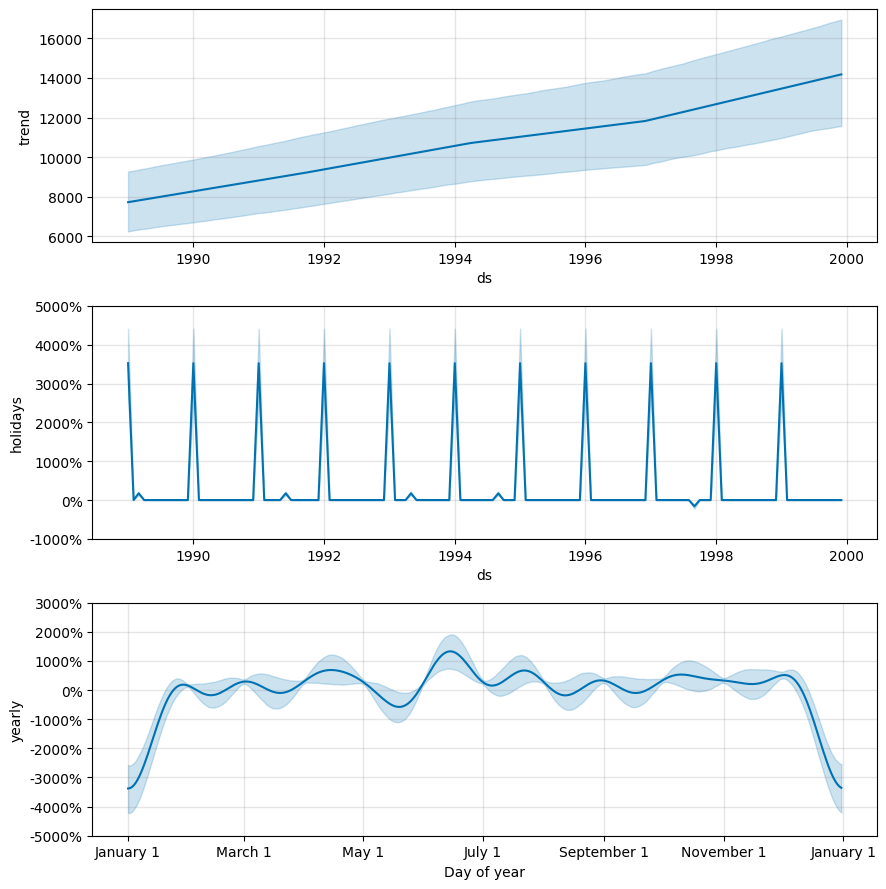
可以看到,预测结果的不确定度降低了,预测结果的形状也发生了变化。